LADR4e Axler Section 3C Matrices
3C Matrices
Representing a Linear Map by a Matrix
Matrices efficient method of using Linear Maps from \(V \rightarrow W\).
Definition 3.29) A \(m \times n\) matrix looks like:
\[A = \pmatrix{A_{1, 1} \ \cdots \ A_{1,n} \\ \vdots \ \qquad \ \vdots \\ A_{n, 1} \ \cdots \ A_{n,n}}\]These are elements in \(\mathbb{F}\).
Definition 3.31) Matrix of a linear map, \(\mathcal{M}(T)\)
\(T \in \mathcal{L}(V, W)\) and \(v_1,...,v_n\) is basis of \(V\) and \(w_1,...,w_m\) a basis of \(W\). The matrix of \(T\) with respect to these basis is \(m \times n\) matrix \(\mathcal{M}(T)\) whose entries \(A_{j,k}\) defined by
\[Tv_k = A_{1, k}w_1 + \cdots + A_{m, k}w_m\]If the bases \(v_1,...,v_n\) and \(w_1,...,w_m\) not clear from context, then notation \(\mathcal{M}(T, (v_1,...,v_n),(w_1,...,w_m))\) used.
The \(k^{th}\) column of \(\mathcal{M}(T)\) consists of the scalars needed to write \(Tv_k\) as a linear combination of \(w_1,...,w_m\):
\[Tv_k = \sum_{j=1}^{m} A_{j,k}w_j\]Looking at the picture, \(w_1,...,w_m\) represents the basis elements of \(W\) and \(v_1,...,v_k,...,v_n\) represents the basis for \(V\). \(Tv_k\) computed by multiplying each entry in \(k^{th}\) column by the corresponding \(w_j\) from left column and then adding up the resulting vectors.
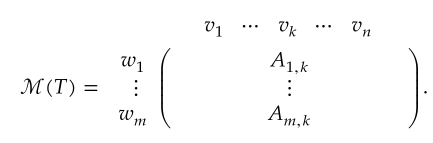
3.23 Example) Matrix of linear map \(\mathbb{F}^2 \rightarrow \mathbb{F}^3\)
\(T \in \mathcal{L}(\mathbb{F}^2, \mathbb{F}^3)\) defined by
\[T(x, y) = (x + 3y, 2x + 5y, 7x + 9y)\]so
\[\mathcal{M}(T) = \pmatrix{ 1 & 3 \\ 2 & 5 \\ 7 & 9}\]Addition and Scalar Multiplication of Matrices
For this part of notes, \(U, V\) and \(W\) are finite-dimensional and each has a basis for each of these vector spaces.
Definition 3.34) Matrix Addition
Sum of two matrices of same size is matrix obtained by adding corresponding entries in the matrices.
Definition 3.35) Matrix of the sum of linear maps
\(S, T \in \mathcal{L}(V, W)\). Then \(\mathcal{M}(S + T) = \mathcal{M}(S) + \mathcal{M}(T)\).
Definition 3.36) Scalar multiplication of a matrix
Multiply each entry in the matrix by the specified scalar.
3.38) Matrix of a scalar times a linear map
\(\lambda \in \mathbb{F}\) and \(T \in \mathcal{L}(V, W)\). Then \(\mathcal{M}(\lambda T) = \lambda\mathcal{M}(T)\).
3.39 Notation) \(\mathbb{F}^{m, n}\)
For \(m\) and \(n\) positive integers, set of all \(m \times n\) matrices with entries in \(\mathbb{F}\) denoted by \(\mathbb{F}^{m, n}\).
3.40) dim \(\mathbb{F}^{m, n}\) = \(m n\)
Matrix Multiplication
Suppose have linear maps \(T \rightarrow U -> V\) and \(S: V \rightarrow W\). Composition \(ST\) from \(U\) to \(V\). Does \(\mathcal{M}(ST)\) = \(\mathcal{M}(S) \mathcal{M}(T)\)? Need to define matrix multiplication first.
3.41 Definition) Matrix multiplication
Let \(A\) be \(m \times n\) matrix and \(B\) be \(n \times p\) matrix. \(AB\) is \(m \times p\) matrix where
Note: I like this definition a lot. Gives a name to a method that’s just arbitrary memorization otherwise. Why can’t I think of these things?
\[(AB)_{j, k} = \sum_{r = 1}^{n} A_{j, r}B_{r, k}\]Matrix multiplication not commutative. \(AB\) not equal to \(BA\) most of the time.
3.43) Matrix of product of linear maps
If \(T \in \mathcal{L}(U, V)\) and \(S \in \mathcal{L}(V, W)\), then \(\mathcal{M}(ST) = \mathcal{M}(S)\mathcal{M}(T)\).
3.44 Notation) \(A_{j,.}, A_{.,k}\)
Suppose \(A\) is an \(m \times n\) matrix
If \(1 \le j \le m\), then \(A_{j,.}\) denote \(1 \times n\) matrix consisting of row \(j\) and \(A\). If \(1 \le k \le n\), then \(A_{.,k}\) denote \(m \times 1\) matrix consisting of column \(k\) of \(A\).
3.45 Example)
If \(A = \pmatrix{8 & 4 & 5 \\ 1 & 9 & 7}\), then
\[A_{2,.} = \pmatrix{1 & 9 & 7} \qquad \mathrm{and} A_{.,2} = \pmatrix{4 \\ 9}\]Another way to think about matrix multiplication:
3.46) Entfy of matrix product equals row times column
\[AB_{j,k} = A_{j,.}B_{.,k}\]3.50) Linear combination of columns
Let A be \(m \times n\) matrix and \(b = \pmatrix{b_1 \\ \vdots \\ b_n}\) is an \(n \times 1\). Then
\[Ab = b_1A_{.,1} + \cdots + b_nA_{.,n}\]By definition of a matrix multiplication.
Next result used for column-row factorization
3.51) Matrix multiplication as linear combinations of columns or rows
Suppose \(C\) is an \(m \times n\) matrix and \(R\) is a \(c \times n\) matrix.
a) If \(k \in {1,...,n}\), then column \(k\) of \(CR\) is a linear combination of the columns of \(C\), with the coefficients of this linear combination coming from column \(k\) of \(R\).
b) If \(j \in {1,...,m}\), then row \(j\) of \(CR\) is a linear combination of the rows of \(R\), with the coefficients of this linear combination coming from row \(j\) of \(C\).
Column-Row Factorization and Rank of a Matrix
3.52 Definition) column rank, row rank
Suppose \(A\) is an \(m \times n\) matrix with entries in \(\mathbb{F}\).
- Column Rank of \(A\) is dimension of the span of the columns of \(A\) in \(\mathbb{F}^{m,1}\).
- Row Rank of \(A\) is dimension of the span of the rows of \(A\) in \(\mathbb{F}^{1,n}\).
3.54 Definition) Transpose, \(A^t\)
\[(A^t)_{k,j} = A_{j,k}\] \[(A + B)^t = A^t + B^t, (\lambda A)^t = \lambda A^t, (AC)^t = C^tA^t\]3.65) Column-row factorization
Let \(A\) be \(m \times n\) matrix with entries in \(\mathbb{F}\) and column rank \(c \ge 1\). Then there exists an \(m \times c\) matrix \(C\) and a \(c \times n\) matrix \(R\), both with entries in \(\mathbb{F}\), such that \(A = CR\).